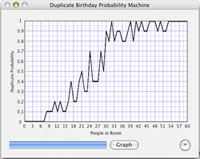
What’s the “Birthday Paradox”? From Wikipedia: The birthday paradox states that if there are 23 or more people in a room then there is a chance of more than 50% that at least two of them will have the same birthday. This means that in a typically-sized school class where the ‘paradox’ is often cited, an even higher probability often applies. For 60 or more people, the probability is already greater than 99%. This is not a paradox in the sense of leading to a logical contradiction; it is a paradox in the sense that it is a mathematical truth that contradicts common intuition. Most people estimate that the chance is much lower than 50%.
If you know of any children (or anybody in general) into math or birthdays, this might be an interesting way to introduce them to genealogy – have them estimate the probabilities of people in your family tree sharing a birthday, and then have them work through the tree to determine if it’s true or not. If they are not aware of the birthday paradox, they might be very surprised.